Soal Transformasi Geometri Kelas 11 – Transformasi geometri adalah salah satu materi yang ada dalam mata pelajaran matematika. Pada umumnya materi geometri sudah diajarkan dari kelas 9 hingga SMA kelas 11. Transformasi Geometri membahas materi mengenai perubahan dari suatu bidang.
Adanya transformasi geometri, sebenarnya terjadi pada kehidupan sehari-hari. Pada Matematika biasanya digambarkan melalui sebuah titik tertentu. Apabila kalian ingin belajar matematika dasar transformasi geometri, maka seharusnya kalian telah sedikit paham mengenai pelajaran Matematika dasar matriks, karena agar dapat menyelesaikan masalah transformasi geometri bisa dilakukan melalui penggunaan matriks.
Dalam penerapan transformasi geometri pada kehidupan sehari-hari tidaklah sedikit, seperti bisa digunakan ketika membuat seni batik atau motif lantai keramik. Belajar serta menggunakan petunjuk-petunjuk dalam transformasi geometri untuk dapat memecahkan masalah bukanlah suatu yang susah.
Apabila kalian mengikuti petunjuk, maka kalian bisa memahami soal-soal transformasi geometri serta menemukan solusi. Pada pembahasan sebelumnya kami juga membahas masih seputar Matematika yakni mengenai contoh soal konversi bilangan.
Soal Transformasi Geometri Kelas 11
Transformasi geometri merupakan materi dalam Matematika yang mempelajari tentang perubahan posisi serta ukuran benda melalui konsep matematis. Terdapat 5 jenis transformasi geometri yang diberikan pada tingkat SMA, seperti : Translasi ( Pergeseran ), Refleksi ( Pencerminan ), Rotasi ( Perputaran ), Dilatasi ( Perubahan Ukuran ), serta Transformasi Matriks.
Dibawah ini kami sajikan beberapa soal mengenai transformasi geometri beserta jawabannya yang telah kami susun secara lengkap.
Soal Pilihan Ganda Transformasi Geometri
Berikut contoh soal transformasi geometri dalam bentuk pilihan ganda beserta jawaban untuk kelas 11 :
1. Apabila jajar genjang MNOP dengan M=(-3,5), N=(4,1), O=(6,8), dicerminkan kepada garis y = −x, maka P yakni…
A. (1,-12).
B. (-12,1).
C. (21,-1).
D. (12,-7).
E. (-7,12).
2. Apabila garis x − 2y − 2 = 0 dicerminkan ke sumbu Y, maka persamaan garis yaitu…
A. 2y + x + 3 = 0.
B. −x − 2y + 3 = 0.
C. −x + 2y + 3 = 0.
D. 2y + x − 3 = 0.
E. 2y − (-x) − 3 = 0.
3. L = (5,-3) dirotasikan (О,180°), maka L…
A. (-5,3).
B. (3,-5).
C. (3,5).
D. (-5,-3).
E. (-3,-5).
4. D = (-2,6) direfleksikan ke garis x = 3, maka bayangan D…
A. (4,6).
B. (-4,6).
C. (-8,6).
D. (6,6).
E. (8,6).
5. Bayangan N = (a,b) kemudian dicerminkan terhadap garis y = -5 menjadi z′(6, −5)
Nilai dari b – a = . . . .
A. 11.
B. 28.
C. 19.
D. 15.
E. −11.
6. Pada segitiga XYZ dengan koordinat sudut X = (2, −1), Y = (6, −2), Z = (5, 2) dirotasi menjadi sejauh 180° dengan pusat (3, 1). Bayangan koordinat sudut segitiga XYZ yaitu…
A. X = (4, 3), Y = (0, 4), Z = (1, 0).
B. X = (3, 4), Y = (4, 0), Z = (0, 1).
C. X = (−4, 3), Y = (-4, 0), Z = (−1, 0).
D. X = (−4, −3),Y = (0, −4), Z = (−1,0).
E. X = (−4, −3),Y = (0,4), Z = (1,1).
7. Apabila garis x − 2y = 5 diputar menjadi sejauh 90° dari (2, 4) diputar berlawanan arah putaran jam, maka persamaannya yakni…
A. 2x + y = −19.
B. 2x + y = 19.
C. x − y = 19.
D. x − y = 19.
E. −x − y = 19.
8. P = (2, -6) dilatasi ke pusat dilatasi O(0,0) dengan faktor dilatasi k = 2, koordinat bayangannya yakni…
A. P’ = (-4, -12).
B. P’ = (-2, -6).
C. P’ = (-4, 12).
D. P’ = (4, -12).
E. P’ = (1, -3).
9. C = (5, −1) dirotasikan ke D = (2, 3) jadi 90° searah dengan jarum jam. Jadi, C adalah…
A. C′ = (−4, −3).
B. C′ = (−5, 1).
C. C′ = (−5, −1).
D. C′ = (−2, 0).
E. C′ = (0, −2).
10. Pada segitiga LUV dengan L = (4, 1), U = (8, 1), V = (5, 8) didilatasi dengan pusat O dan faktor skala 3 menghasilkan segitiga L’U’V’. Perbandingan luas segitiga LUV dengan luas segitiga L’U’V’ ialah…
A. 1 : 5.
B. 1 : 6.
C. 1 : 7.
D. 1 : 8.
E. 1 : 9.
Jawaban
- B
- E
- A
- E
- E
- A
- B
- D
- B
- E
Soal Essay Transformasi Geometri
Berikut contoh soal transformasi geometri dalam bentuk essay dan jawabannya untuk kelas 11 :
1. Tentukan bayangan dari A = (3, 7), apabila direfleksikan ke sumbu X kemudian dilatasi pada pusat (0, 0) menggunakan skala 2…
2. A = (-4, 7) direfleksikan ke garis y = -x. Maka koordinat A adalah…
3. Tentukan bayangan dari L = (3, 2), apabila dilatasikan ke pusat (-1, -2) menggunakan skala -3…
4. Tentukan koordinat dari titik D jika D’ = (13, -20) adalah bayangan titik D karena translasi C = (10, -7), yakni…
5. Apabila garis Y = X + 5 ditranslasikan oleh (23), maka persamaan bayangannya adalah…
Jawaban
1. Catatan :
A’ = (p, q) merupakan bayangan titik A jika direfleksikan terhadap sumbu x, maka
A’ = (r, s) merupakan bayangan titik A’ jika dilatasikan pada pusat (0, 0) dengan skala 2.
Refleksi titik A di sumbu x yaitu :
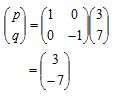
Dilatasi titik A’ ke pusat (0, 0) menggunakan skala 2 :
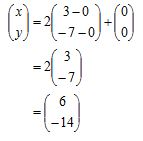
Jadi, titik A = (3, 7) apabila direfleksikan ke sumbu x kemudian dilatasi pada pusat (0, 0) menggunakan skala 2 yakni (6, -14)
2. A’ = (x, y) merupakan koordinat A, maka :
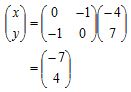
Maka, koordinat bayangan titik A adalah (-7, 4).
3. Catatan :
L’ = (x, y) merupakan bayangan titik L.
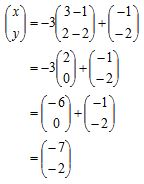
Bayangan titik L adalah (-7, -2).
4. D = (x, y), jadi :
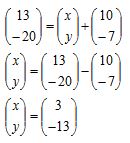
koordinat titik D adalah (3, -13).
5. Catatan :
(X′Y′) = (XY) + (23)
Jadi :
X’ = X+2 -> X = X’-2
Y’ = Y+3 -> Y = Y’-3
Dengan menggantikan X = X’-2 dan Y = Y’-3 ke persamaan garis, hasilnya :
Y’-3 = (X’ – 2)+5
Y’-3 = X’+3
Y’ = X’ + 6
Persamaan bayangan garis Y = X+5 dari translasi (23) adalah Y = X+6.
Download Soal
Kami juga menyediakan soal lainnya dalam bentuk file PDF dan bisa di unduj di bawah ini :
Kesimpulan
Demikian penjelasan dari orangbaik.org mengenai soal transformasi geometri kelas 11 dan jawaban. Semoga dengan adanya artikel ini peserta didik lebih giat lagi untuk belajar mengenai mata pelajaran Matematika. Dengan cara sering berlatih mengerjakan soal maka akan menjadikan para siswa mengetahui cara memecahkan masalah dan menemukan wawasan baru. Sekian terimakasih.




