Rumus Gradien Tegak Lurus – Selain mendapati materi statistika, para siswa kelas 8 SMP juga akan mempelajari Persamaan Garis Lurus. Di dalam materi tersebut terdapat beberapa materi yang bakal dipelajari siswa, salah satunya yakni Gradien Tegak Lurus.
Gradien Tegak Lurus sendiri bisa dianalogikan secara sederhana sebagai bangunan tembok. Di mana bangunan tersebut perlu dibangun secara terukur dan sangat presisi. Di situ diperlukanlah Rumus Gradien Tegak Lurus yang mana dibutuhkan pekerja supaya tegak lurus.
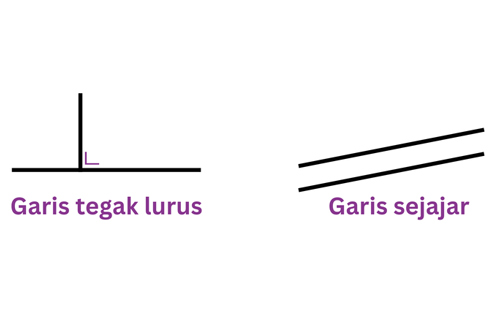
Dengan adanya Rumus Gradien Tegak Lurus, nantinya bisa tegak lurus dengan garis di bawahnya yang mana diketahui seperti huruf L. Apabilai garis tidak sejajar, hal itu bisa mengakibatkan kemiriangan dan bisa terjadi bangunan rusak atau roboh.
Lalu bagaimanakah Rumus Gradien Tegak Lurus dalam ilmu Matematika kelas 8 SMP? Agar para siswa tahu dan paham, Orangbaik.org akan menjelaskannya di artikel ini. Bagi kamu yang penasaran bisa ikuti pembahasan di bawah ini hingga selesai.
Beberapa Rumus Gradien Tegak Lurus
Berdasarkan sumber yang didapat, gradien disebut sebagai nilai kemiringan atau kecondongan suatu garis dan membandingkan antara dua komponen yakni Y (ordinat) dengan X (absisi). Adapun dari gradien tersebutlah yang menentukan tingkat kemiringan pada suatu garis dalam koordinat cartesius.
Gradien garis sendiri bisa miring ke kanan, ke kiri, curam, ataupun landai. Nilai kemiringan pada dgaris tergantung darri nilai komponen X dengan komponen Y. Agar bisa mengetahui tingkat kemiringan, ada rumus gradien. Penggunaan rumus inipun penting supaya bangunan yang dibandung memiliki kemiringan pas sehingga tidak mencelakai orang.
Dikutip dari Katadata, ada dua sifat gradien dari dua garis lurus yakni dua garis sejajar dan dua garis tegak lurus. Untuk mengetahui hal itu akan dijelaskan di bawah ini.
Dua Garis Sejajar
Dikatakan garis sejajar jika garis A dan B salin sejajar, keduanya memiliki nilai gradien yang sama dan bisa dinyatakan sebagai berikut.
mA = mB
Dua Garis Tegak Lurus
Sedangkan dua garis dikatakan tegak lurus apabila garis A dan B saling tegak lurus. Untuk mengetahui gradien pada dua garis tersebut, maka bisa ditemukan dengan rumus berikut ini.
mA x mB = -1
Nah, itulah dua rumus yang secara umum pada materi gradien. Adapun untuk gradien tegak lurus merupakan dua garis yang terlihat tegak lurus. Selain itu, gradien tegak lurus juga disebut dua garis berpotongan dan pada titik potongnya membentuk siku-siku sebesar 90°.
Jika dua garis tegak lurus dikalikan akan menghasilkan nilai -1. Untuk mengetahui gradiennya, maka bisa dicari dengan rumus:
y = mx + c
Kumpulan Contoh Soal Gradien Tegak Lurus
Supaya lebih paham rumusnya, Orangbaik akan memberikan contoh soalnya. Di bawah ini penulis telah sediakan beberapa contoh soal yang bisa kita pelajari bersama yang mana sudah terdapat pembahasannya. Berikut beberapa contoh soal menghitung gradien tegak lurus.
1. Diketahui garis lurus y=3x+2. Tentukan gradien dari garis yang tegak lurus dengan garis ini dan tentukan persamaannya!
Pembahasan:
Gradien dari garis y =3x+2y=3x+2 adalah 3m=3. Gradien tegak lurus akan memiliki hubungan negatif terhadapnya, yaitu −1m=−1/3. Persamaan garis tegak lurus dapat dituliskan dalam bentuk y=−1/3x+c, di mana c adalah konstanta. Persamaan ini menggambarkan garis yang tegak lurus dengan garis y=3x+2.
2. Diketahui garis dengan persamaan 2x−5y=10. Temukan gradien dari garis yang tegak lurus dengan garis ini dan tentukan persamaannya!
Pembahasan:
Untuk menemukan gradien tegak lurus, kita perlu menukar koefisien x dan y dalam persamaan garis. Persamaan 2x−5y=10 memiliki gradien m=2/5. Gradien tegak lurusnya adalah −1m=−5/2. Persamaan garis tegak lurus dapat dituliskan sebagai y=−5/2x+c.
3. Diketahui garis y=−4/7x+3. Tentukan gradien dari garis yang tegak lurus dengan garis ini dan tentukan persamaannya.
Pembahasan:
Gradien dari garis y=−4/7x+3 adalah m=−4/7. Gradien tegak lurusnya adalah −1m=7/4. Persamaan garis tegak lurus dapat dituliskan sebagai y=7/4x+c.
4. Diketahui garis dengan persamaan 3x+2y=12. Cari gradien dari garis yang tegak lurus dengan garis ini dan tentukan persamaannya.
Pembahasan:
Untuk menemukan gradien tegak lurus, kita perlu menukar koefisien x dan y dalam persamaan garis. Persamaan 3x+2y=12 dapat diubah menjadi y=−3/2x+6y, sehingga gradiennya adalah m=−3/2. Gradien tegak lurusnya adalah −1m=2/3. Persamaan garis tegak lurus dapat dituliskan sebagai y=2/3x+c.
5. Diketahui garis y=5x−1. Tentukan gradien dari garis yang tegak lurus dengan garis ini dan tentukan persamaannya!
Pembahasan:
Gradien dari garis y=5x−1y=5x−1 adalah m=5. Gradien tegak lurusnya adalah −1m=−1/5. Persamaan garis tegak lurus dapat dituliskan sebagai y=−1/5x+c.
Nah, itulah beberapa contoh soal yang bisa dijadikan sebagai bahan belajar materi Gradien Tegak Lurus. Apabila masih kurang paham, kamu bisa tanyakan kepada guru saat di jam pelajaran. Atau, kalian bisa download modul materi Gradien. Di dalam modul tersebut terdapat penjelasan materi, rumus, dan pembahasan soalnya. Silakan langsung download saja di link bawah ini.
Akhir Kata
Dari keseluruhan pembahasan di atas, bisa disimpulkan bahwasanya materi gradien sangatlah penting dipakai dalam hal sehari-hari. Contohnya seperti pembangunan bangunan. Untuk mendapatkan tingkat tegak lurus 90° maka dipakailah rumus.
Demikian pembahasan dari Orangbaik.org terkait Rumus Gradien Tegak Lurus. Di pembahasan juga kamu menyertakan materinya secara jelas dan rinci. Setidaknya dari pembahasan artikel ini bisa membantu para siswa maupun guru supaya bisa menguasai materi Gradien.
Sumber Gambar: Admin Orangbaik.org