Contoh Soal Persamaan Eksponen dan Jawabannya – Matematika menjadi salah satu Mata Pelajaran yang membutuhkan konsentrasi tinggi untuk dipahami. Semakin tinggi jenjang pendidikan, maka semakin sulit materi Matematika yang diberikan.
Contoh, ketika duduk di bangku SMA atau SMK kelas 10 kalian bakal menemui materi Persamaan Eskponen. Contoh soal Persamaan Eksponen dan jawabannya yang bakal kami sajikan berikut ini mungkin bisa membantu kalian dalam menguasai materi tersebut.
Sama seperti materi Fungsi Invers, Fungsi Komposisi yang juga bakal diajarkan di SMA dan SMK, materi Persamaan Eksponen juga bisa dijadikan soal UN Matematika nanti di kelas 12. Oleh karena itu, mulai dari sekarang kalian perlu rajin-rajin mempelajari contoh soal Persamaan Eksponen dan jawabannya.
Di bawah ini kami berhasil merangkum beberapa contoh soal Persamaan Eksponen dan jawabannya untuk kelas 10. Selain itu, kami juga bakal menjelaskan sedikit tentang pengertian dari Persamaan Eksponen, rumus yang digunakan dan lain sebagainya.
Contoh Soal Persamaan Eksponen dan Jawabannya

Selain belajar Logaritma, bagi kalian para siswa-siswa kelas 10, pada Mata Pelajaran Matematika juga akan menjumpai pembelajaran tentang Persamaan Eksponen. Materi ini merupakan bentuk perkalian suatu bilangan dengan dirinya sendiri sebanyak pangkatnya.
Untuk memahami materi ini, kalian perlu mengetahui rumus atau sifat-sifat yang berlaku. Berikut adalah sifat-sifat yang terdapat di Persamaan Eksponen :
- Contoh a > 0 dan a ≠ 1.
- Jika af(x) = ag(x) maka f(x) = g(x)
- Contoh a, b > 0 dan a, b ≠ 1.
- Jika af(x) = bf(x) maka f(x) = 0
- Contoh a, b > 0 dan a, b ≠ 1.
- Jika af(x) = bg(x) maka log af(x) = log bg(x)
- Jika f(x)g(x) = 1 maka
(1) f(x) = 1
(2) f(x) = -1, dengan syarat g(x) genap
(3) g(x) = 0, dengan syarat f(x) ≠ 0
- Jika f(x)h(x) = g(x)h(x) maka
(1) f(x) = g(x)
(2) f(x) = -g(x), dengan syarat h(x) genap
(3) h(x) = 0, dengan syarat f(x) ≠ 0 dan g(x) ≠ 0
- Jika f(x)g(x) = f(x)h(x) maka
(1) g(x) = h(x)
(2) f(x) = 1
(3) f(x) = -1, g(x) dan h(x) keduanya genap/ganjil
(4) f(x) = 0, g(x) dan h(x) keduanya positif
Setelah mengetahui rumus Persamaan Esponen, sekarang kita lanjut ke contoh soal Persamaan Eksponen dan jawabannya. Berikut kami berhasil mengumpulkan contoh soal dilengkapi jawaban dan pembahasan tentang materi tersebut dari beberapa sumber yang
Contoh 1
Tentukan nilai b (dalam p) dari Persamaan Eksponen berikut :
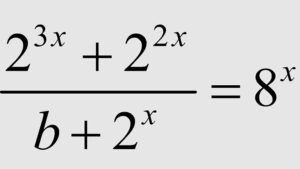
Jawabannya :

nilai b (dalam p) dari persamaan diatas adalah b = 1 – p.
Contoh 2
Contoh 3
Jika 22x-7 = 81-x, coba tentukan penyelesaian dari Persamaan Ekponensial nya :
Jawabannya:
Pertama-tama yang perlu kamu lakukan yaitu menyamakan basis pada kedua ruas [ruas kanan dan ruas kiri] seperti berikut:
22x-7 = 81-x
22x-7 = (23)1-x
22x-7 = 23-3x
2x – 7 = 3 – 3x
5x = 10
x = 2
Sehingga kita peroleh x = 2
Contoh 4
Jika 3ˣ⁻²ʸ = 1/81 dan 2ˣ⁻ʸ = 16, maka nilai x + y
Jawab:
Dengan menggunakan sifat-sifat persamaan eksponen, maka
3ˣ⁻²ʸ = 1/81
3ˣ⁻²ʸ = 1/3⁴
3ˣ⁻²ʸ = 3⁻⁴ ……………………… pers 1
2ˣ⁻ʸ= 16
2ˣ⁻ʸ = 2⁴
x – y = 4 ………………………….. pers 2
Dari pers 1 dan pers 2, diperoleh
x – 2y = -4
x – y = 4
_ –
-y = -8
y = 8
Nilai y dapat kita subsitusikan ke pers 1 atau 2, maka
x – 2y = -4
y = 8
x – 2(8) = -4
x = -4 + 16
x = 12
atau
x – y = 4
x – (8) = 4
x = 4 + 8
x = 12
Jika nilai x = 12, dan nilai y = 8
Maka, x + y = 12 + 8 = 20
Contoh 5
Jika a dan b merupakan bilangan bulat positif yang memenuhi ab = 220 – 219 , maka berapa nilai a + b ?
Jawabannya:
Dari sifat pangkat dan sifat distributif, diketahui:
ab = 220 – 219
ab = 219 . 2 – 219
ab = 219 . (2-1)
Jika a = 2 dan b = 9 maka hasil a + b = 2 + 19 = 21
Contoh 6
Tentukan penyelesaian dari persamaan eksponensial berikut ini 22x-7 = 81-x
Jawabannya:
22x-7 = 81-x
22x-7 = (23)1-x
22x-7 = 23-3x
Jadi, cara menentukan nilai x-nya seperti berikut ini.
2x – 7 = 3 – 3x
5x = 10
x = 2
Sehingga kita peroleh x = 2
Contoh 7
Jika a dan b bilangan bulat positif yang memenuhi ab = 220 – 219 , maka nilai a + b = …
Jawabannya:
Dengan menggunakan sifat pangkat dan sifat distributif, diperoleh:
ab = 220 – 219
ab = 219 . 2 – 219
ab = 219 . (2-1)
Dari sini, diperoleh a = 2 dan b = 9 sehingga a + b = 2 + 19 = 21
Contoh 8
Tentukan himpunan penyelesaian dari 9 x²+x = 27 x²-1
Jawabannya:
9 x²+x = 27 x²-1
3 2(x²+x) = 3 3(x²-1)
2 (x2+x) = 3 (x2-1)
2×2 + 2x = 3×2 – 3
x2 – 2x – 3 = 0
(x – 3) (x + 1) = 0
x = 3 atau x = -1
Jadi, himpunan penyelesaian dari soal diatas adalah { -1,3 }
Contoh 9
Tentukan nilai x dari Persamaan Eksponen berikut.
25 x+2 = (0,2) 1-x
Jawabannya:
25 x+2 = (0,2) 1-x
52(x+2) = 5 -1(1-x)
2x + 4 = -1 + x
2x – x = -1 – 4
x = -5
Jadi nilai x yang diperoleh adalah -5
Contoh 10
Tentukan nilai x dari persamaan 3⁵ˣ⁻¹ – 27ˣ⁺³ = 0
Jawabannya:
3⁵ˣ⁻¹ – 27ˣ⁺³ = 0
3⁵ˣ⁻¹ = (3³)ˣ⁺³
3⁵ˣ⁻¹ = 3³ˣ⁺⁹
5x-1 = 3x + 9
2x = 10
x = 5
Download Kumpulan Soal Persamaan Eksponen PDF
Diatas merupakan sedikit contoh soal Persamaan Eksponen untuk kelas 10 yang kami rangkum dari beberapa website materi MTK. Jika contoh soal diatas belum cukup untuk mempelajari materi tentang Persamaan Eksponen, maka kalian bisa simak kumpulan contoh soal Persamaan Eksponen dan jawabannya di bawah ini :
Kalian bisa download file diatas agar bisa dipelajari secara Offline. File kumpulan soal diatas memiliki format PDF.
KESIMPULAN
Demikianlah informasi dari Orangbaik.org tentang contoh soal Persamaan Eksponen dan jawabannya. Melalui kumpulan contoh soal diatas kalian bisa meningkatkan kemampuan dalam mengerjakan soal Matematika dari materi Persamaan Eksponen.
Diatas juga kami sebutkan bahwa soal-soal tentang Persamaan Eksponen mungkin bakal dijumpai pada soal UN Matematika maupun ASBN di SMA dan SMK. Jadi, pastikan kalian mempelajari materi ini dengan baik.
sumber gambar :
- sonora.id
- Channel Youtube Matematika Hebat
- elearning.smansadompu.com



