Contoh Soal Integral Substitusi – Materi Integral subtitusi ini sering muncul dalam soal ujian nasional maupun ujian sekolah sehingga, banyak murid mencari materi ini. Mata pelajaran Matematika adalah salah satu pelajaran yang wajib dipelajari.
Walaupun Matematika menjadi pelajaran wajib, tetapi sebagian besar siswa menghindarinya karena dirasa sulit. Disebabkan, pelajaran ini dirasa menjadi pelajaran yang sulit dipelajari karena harus menghitung, menghafal rumus, dan lainnya.
Saat di sekolah materi yang dipelajari hanya dasarnya saja, namun tingkat kesulitan matematika di setiap tingkat akan bertambah. Pada saat kalian berada di tingkat SMA kalian akan belajar mengenai materi integral. Di materi ini akan mempelajari tentang integral substitusi dan parsial.
Pada kesempatan kali ini kami akan menjelaskan mengenai integral substitusi untuk para siswa dalam belajar. Kami juga sebelumnya pernah membahas masih tentang mata pelajaran Matematika yakni mengenai contoh soal pembagian ratusan mungkin bisa kalian jadikan referensi sebelum mengerjakan ulangan ataupun UAS.
Contoh Soal Integral Substitusi
Integral Substitusi yakni suatu metode atau cara ketika menyelesaikan permasalahan integral. Sesuai pembahasan diatas, kalian bisa melalui substitusi untuk menyederhanakan permasalahan tersebut. Pada pembahasan sebelumnya dan bisa untuk referensi kalian kami juga membagikan tentang soal bilangan berpangkat.
Contoh a merupakan fungsi yang terdiferensial dan F merupakan anti turunan dari f . Jadi :
∫ f (a(x)) a'(x) dx= F(a(x)) + C
Dibawah ini contoh soalnya :
y = (x²+3x+5) 9
1. Tentukan turunannya !
Jawaban :
y’= 9 (x² + 3x + 5) 8 (2x + 3)
2. Tentukan hasil substitusi dari :
∫ (3x+4) √3+4 dx
Jawaban :
u = 3x + 4 -> du/dx = 3
= ⅓ du
Kemudian hasil disubstitusi dalam soal integral menjadi :
∫(3x + 4) √3x + 4 dx = ∫u √u ⋅
⅓ du = ⅓ ∫u 3/2 du
=⅓ . 1/ 3/2 + 1 u 3/2 +1 + C
=⅓ . ⅖ u 5/2 + C
=2/15 (3x + 4)2 √3x + 4 + C
3. Tentukan hasil substitusi dari :
4x³ (x⁴-1)2 dx
Jawaban :
u = x⁴-1
u = x⁴-1 -> du/dz = 4x³
du = 4x³ dx
∫ 4x³ (x⁴-1)2 dx = ∫ (x⁴-1)2.4x³ dx
= ∫u²du = ⅓ u³ + C
= (⅓ 9x⁴ – 1)3 + C
4. Tentukan substitusi dari ∫ √3x dx !
∫ √3x dx = ∫ √u du : 3
= ⅓ ∫ u½ du
= ⅓ . u3/2 : 3/2 + C
= 2/9 u3/2 + C
= 2/9 (3x)3/2 + C
u = 3x
5. Berapa hasil dari substitusi∫ (2x-1) (x²-x+3)³ dx!
Substitusi u :
∫ (2x-1)(x²-x+3)³ dx = ∫ u³ du
∫ (2x-1)(x²-x+3)³ dx = ¼ u⁴ + C
∫ (2x-1)(x²-x+3)³ dx = ¼ (x²-x+3)⁴ + C
Penjelasan Integral
Integral bisa disebut sebagai kebalikan atau invers dalam operasi turunan. Integral dibagi menjadi 2 bentuk yakni : Integral Tentu dan Integral Tidak Tentu. Integral tentu diartikan sebagai jumlah sebuah daerah yang terkena batas dari kurva atau persamaan tertentu. Sementara, Integral tidak tentu dapat diartikan sebagai kebalikan atau invers dari turunan.
Bentuk Baku Pada Integral Substitusi
Pada penjelasan diatas, kalian sudah mempelajari tentang pengertian dan contoh soal integral. Selanjutnya kalian akan belajar mengenai teknik-teknik yang ada dalam materi integral. Teknik-teknik tersebut terdiri dari teknik Integral dengan Substitusi, Integral Parsial, Integral Trigonometri, Integral Substitusi Lain, serta Integral Fungsi Rasional yakni hasil dibagi dua fungsi suku banyak atau polinom. Agar bisa menggunakan substitusi dengan hasil yang sesuai, maka kalian harus mengetahui bentuk integral sebanyak-banyaknya. Dibawah ini beberapa contoh bentuk baku integral dan hasil.
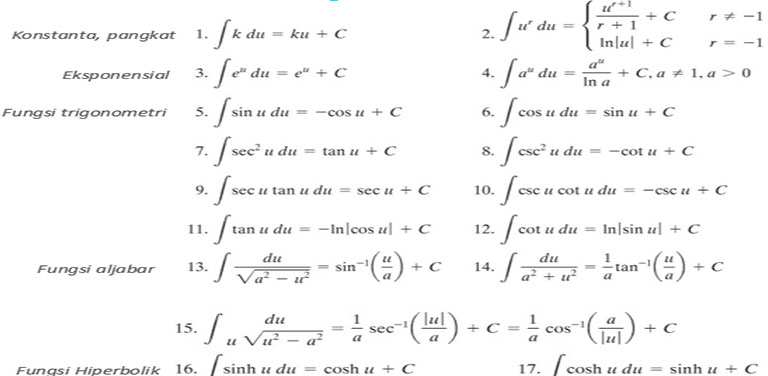
Substitusi pada Integral Tentu
Substitusi pada integral tentu tidak jauh berbeda dari substitusi pada integral tidak tentu, namun sebelumnya kalian jangan melupakan untuk mengganti batas pengintegralannya.
Contoh :
g memiliki turunan dengan kontinu di (a,b), dan f merupakan kontinu di range g. Jadi :

Substitusi pada Integral Tidak Tentu
Apabila kalian menjumpai sebuah integral tidak tentu. jika berbentuk baku, maka bisa cepat ditulis hasilnya. Namun jika tidak, maka harus mencari suatu substitusi yang akan menggantinya jadi sebuah bentuk baku. Jika dalam substitusi pertama, kalian tidak dapat memperoleh bentuk baku, kalian bisa mencoba dengan cara lain.
Contoh :
g merupakan fungsi dan bisa didiferensialkan, serta F adalah anti turunan dari f. Jadi, apabila u = g(x)

Contoh Fungsi dari Integral
Integral berguna di beragam bidang. Dalam bidang Matematika dan Teknik, integral dimanfaatkan untuk menghitung volume benda serta luas kurva. Di bidang Fisika, integral dimanfaatkan untuk menghitung serta menganalisis arus listrik, medan magnet, dan sebagainya. Pada bidang Ekonomi, integral berfungsi untuk menentukan persamaan serta fungsi Ekonomi, Konsumsi, Marginal. Kami juga membagikan contoh soal integral substitusi dalam bentuk file pdf yang bisa di unduh berikut ini :
Kesimpulan
Demikian penjelasan dari orangbaik.org mengenai contoh soal integral substitusi beserta jawaban dan file pdf yang bisa di unduh. Diharapkan dengan adanya artikel ini para siswa lebih rajin lagi untuk belajar mengenai mata pelajaran Matematika. Dengan cara sering berlatih mengerjakan soal maka akan menjadikan para siswa mengetahui cara memecahkan masalah serta menemukan wawasan baru. Sekian terimakasih.




