Contoh Soal Faktorial – Dalam pelajaran matematika, banyak pernyataan atau cara menuliskan notasi matematis melalui simbol. Faktorial merupakan salah satu dari sekian banyak notasi yang mampu mempersingkat penulisan soal perkalian.
Ketika belajar tentang ilmu berhitung seperti perkalian tentu saja matematika akan terlintas di benak kalian. Di sekolah dasar, siswa diajarkan bahwa mengalikan banyak angka berurutan perlu dituliskan secara lengkap. Namun berbeda di SMP serta SMA, karena contoh soal faktorial digunakan untuk mempersingkatnya.
Meskipun pada dasarnya faktorial hanyalah simbol penggambaran operasi perkalian, tetapi masih banyak murid merasa kesulitan saat harus mengerjakan contoh soal faktorial terutama apabila bentuknya berupa pecahan.
Oleh karena itu, Orangbaik.org hendak membahas mengenai contoh soal faktorial baik bentuk dasarnya hingga faktorial pecahan. Selain contoh soalnya, di sini kami juga akan membagikan jawabannya dan penyelesaiannya.
Ringkasan Materi Seputar Faktorial
Pada penjelasan di atas sudah disinggung bahwa faktorial dengan simbol (!) merupakan cara penulisan atau notasi ilmiah dalam perkalian bilangan cacah berurutan. Agar lebih mudah memahaminya simaklah beberapa contoh faktorial sederhana berikut ini :
4! = 4×3×2×1
6! = 6×5×4×3×2×1
Penjelasan faktorial di atas umumnya dipelajari ketika kalian belajar mengenai faktorial di tingkat SMP ataupun MTs.
Jenis Faktorial
Jika kalian sudah menginjak di jenjang pendidikan lebih lanjut mulai dari SMA sederajat sampai dengan perguruan tinggi maka ilmu faktorial terbagi menjadi 3 (tiga) jenis serta terdapat juga ketentuan khusus lainnya. Berikut adalah ketentuan khusus terkait faktorial :
- Hasil dari faktorial nol atau 0! adalah 1.
- Faktorial terbagi menjadi jenis terdefinisi serta tak terdefinisi.
- Faktorial dapat dinotasikan dengan bentuk n!.
Dimana seluruh ketentuan faktorial tersebut berkaitan dengan jenis faktorial, yaitu :
1. Faktorial Terdefinisi
Jenis faktorial ini mempunyai batasan yang jelas dalam besarnya nilai perkaliannya karena hanya memuat bilangan asli. Contoh :
- 8! = 8×7×6×5×4×3×2×1 = 40320
- 5!/3! = (5×4×3×2×1)/(3×2×1) = 20
atau dapat dituliskan sebagai berikut
5!/3! = (5×4×3!)/(3!) = 5×4 = 20
2. Faktorial Tak Terdefinisi
Jenis faktorial tak terdefinisi artinya bilangan yang dihitung belum dijelaskan dalam notasinya. Faktorial jenis ini dapat dituliskan secara terbalik yakni dari bilangan terkecil sampai tak hingga, namun tentunya masih dalam batasan bilangan asli. Contoh :
- n! = n×(n-1)×(n-2)….×(n-r+1)×(n-r)
dengan n dan r bilangan asli.
Contoh Soal Faktorial dan Penyelesaiannya
Supaya lebih mudah dalam memahami gambaran soal faktorial maka sebaiknya langsung saja simak contoh soalnya. Berikut adalah beberapa contoh persoalan faktorial yang telah kami siapkan beserta jawaban, pembahasan
Contoh Soal 1
Selesaikanlah operasi faktorial penjumlahan, pengurangan serta perkalian berikut ini!

Jawaban & Pembahasan :
a) 7! = 7×6×5×4×3×2×1 = 5.040
b) Perhitungan faktorial pengurangan
5!-3! = (5×4×3!) – (3!) = (5×4-1)(3!) = 19×3! = 19×6 = 114
c) Perhitungan faktorial penjumlahan
3!+4! = (3!)+(4×3!) = (1+4)(3!) = 5×3! = 5×6 = 30
d) Perhitungan faktorial perkalian
3!×4! = (3!)×(4×3!) = 4×(3!)2 = 4×(6)2 = 4×36 = 144
Contoh Soal 2
Selesaikanlah operasi faktorial bentuk pembagian berikut ini!

Jawaban & Pembahasan :
a) 5!/2! = (5×4×3×2!)/(2!) = 5×4×3 = 60
b) 8!/(5!×3!) = (8×7×6×5!)/(5!×3!) = 8×7×6/(3!) = 8×7×6/6 = 48
c) 12!/(8!×2!×3!) = (12×11×10×9×8!)/(8!×12) = 12×11×10×9/(12) = 990
d) 50!/(48!×2!) = (50×49×48!)/(48!×2) = 25×49 = 1225
Contoh Soal 3
Tentukan bentuk paling sederhana dari faktorial pecahan di bawah!
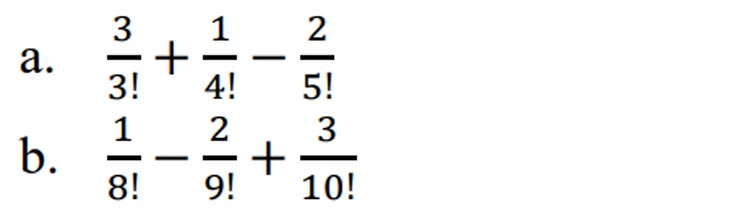
Jawaban & Pembahasan :
a) (3/3!) + (1/4!) – (2/5!)
Samakan lebih dulu penyebutnya sehingga
(3×4×5/5!) + (1×5/5!) – (2/5!) = (60/5!) + (5/5!) – (2/5!) = (60+5-2)/5! = 63/5! = 63/120
b) (1/8!) – (2/9!) + (3/10!) = [(10×9) – (2×10) + 3]/10! = (90-20+3)/10! = 73/10!
Untuk soal faktorial pecahan seperti di atas biasanya boleh dijawab dengan 73/10! saja, kecuali mengerjakannya menggunakan kalkulator.
Contoh Soal 4
Carilah masing-masing nilai n dalam beberapa faktorial di bawah!
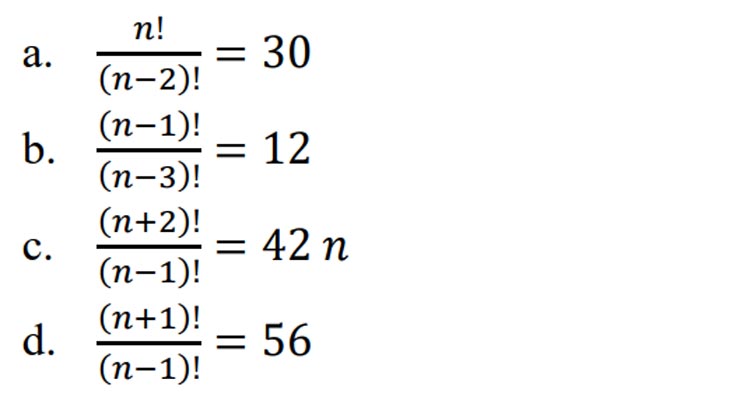
Jawaban & Pembahasan :
Sebelum mulai mengerjakan soal dengan n faktorial, ingatlah bahwa urutan n faktorial adalah n×(n-1)×(n-2)….×(n-r+1)×(n-r)
a) n!/(n-2)! = 30
⇔ [n×(n-1)×(n-2)!]/(n-2)! = 30
⇔ n×(n-1) = 30
⇔ n2-n = 30
⇔ n2-n-30 = 0
Selanjutnya lakukan penarikan akar sehingga didapatkan
(n+5)(n-6) = 0
Maka artinya n=(-5) atau n=6, tapi karena harus bilangan asli maka n pasti bernilai 6.
b) (n-1)!/(n-3)! = 12
⇔ [(n-1)×(n-2)×(n-3)!]/(n-3)! = 12
⇔ (n-1)×(n-2) = 12
⇔ n2-3n+2 = 12
⇔ n2-3n-10 = 0
Selanjutnya lakukan penarikan akar sehingga didapatkan
(n+2)(n-5) = 0
Maka artinya n=(-2) atau n=5, tapi karena harus bilangan asli maka n pasti bernilai 5.
c) (n+2)!/(n-1)! = 42n
⇔ [(n+2)×(n+1)×n×(n-1)!]/(n-1)! = 42n
⇔ (n+2)×(n+1)×n = 42n
⇔ (n+2)×(n+1) = 42
⇔ n2+3n+2 = 42
⇔ n2+3n-40 = 0
Selanjutnya lakukan penarikan akar sehingga didapatkan
(n+8)(n-5) = 0
Maka artinya n=(-8) atau n=5, tapi karena harus bilangan asli maka n pasti bernilai 5.
d) (n+1)!/(n-1)! = 56
⇔ [(n+1)×n×(n-1)!]/(n-1)! = 56
⇔ (n+1)×n = 56
⇔ n2+n = 56
⇔ n2+n-56 = 0
Selanjutnya lakukan penarikan akar sehingga didapatkan
(n+8)(n-7) = 0
Maka artinya n=(-8) atau n=7, tapi karena harus bilangan asli maka n pasti bernilai 7.
Karena nantinya faktorial akan berhubungan dengan materi peluang seperti permutasi dan kombinasi, maka ada baiknya bila kalian juga mempelajari tentang Contoh Soal Kombinasi.
Kesimpulan
Berdasarkan penjelasan dari Orangbaik.org terkait contoh soal faktorial di atas bisa dipahami bahwa persoalan faktorial sebenarnya cukup sederhana. Hanya saja memang membutuhkan ketelitian dan pemahaman mengenai sifat-sifat operasi matematika.




