60 Contoh Soal Bilangan Berpangkat Beserta Jawabannya

Contoh Soal Bilangan Berpangkat – Tahukah anda apa itu bilangan berpangkat? salah satu bilangan di dalam mata pelajaran matematika yaitu bilangan berpangkat, berikut adalah pengertian berpangkat. Bilangan berpangkat yaitu suatu susunan bilangan yang dikalikan dengan pangkat tertentu. Contohnya bilangan x dikalikan dengan y, maka bilangan x secara berulang-ulang sesuai pada bilangan y.

Manfaat dari kita mempelajari matematika khususnya bilangan berpangkat adalah untuk : Mengetahui data jumlah penduduk, Data untuk menghitung angka kelahiran dan juga kematian, dan juga data-data yang lainnya. Bilangan berpangkat mempunyai berbagai jenis yakni : bilangan pangkat positif, bilangan pangkat negatif, bilangan pangkat nol, dan bilangan dalam bentuk akar. Cukup berbeda dengan contoh soal konversi bilangan yang mempunyai rumus tersendiri.

Bilangan berpangkat terdiri atas :

• Bilangan Pangkat Bulat Positif.
• Bilangan Pangkat Bulat Negatif.
• Bilangan Pangkat Dengan Pangkat Nol.
• Bilangan Pangkat Dalam Bentuk Akar.

Dibawah ini adalah beberapa kumpulan contoh soal dari bilangan berpangkat yang ada dalam Matematika beserta kunci jawabannya.

Contoh Soal Bilangan Berpangkat

1. Sederhanakan operasi aljabar berikut ini:

a.y3 x 2 y7 x (3y)²
b.3m3 x (mn)4
c.(2×3) x 3(x2 y2)3 x 5y4

Jawaban soal a
y3 x 2y7 x (3y)2 = y3 x 2y7 x 9y2
=(2 x 9)y 3+7+2
=(2 x 9)y12
=18 y12

Jawaban soal b
3m3 x (mn)4 = 3m3 ´ m4n4
=3m3+ 4 n4
=3m7 n4

Jawaban soal c
(2×3) x 3(x2 y 2 )3 x 5y4 = (2×3 ) x 3(x2x3 y 2×3 ) x 5y 4
=(2×3 )x 3(x6 y6 ) x 5y4
=(2×3 ) x 3x 6 x y6 x 5 y4
=(2 x 3 x 5) x3+6 y 6+4
=30×9 y10

2. Hasil dari 4 pangkat 3/2 x 27 pangkat 1/3 adalah ?

3. Hasil dari 32 pangkat 1/5 adalah ?

4. Hasil dari (64)^-1/3 adalah ?

5. Nilai dari [5 per 10 pangkat 0] + ( 5 per 10 pangkat 1) + (5 per 10 pangkat 2) adalah

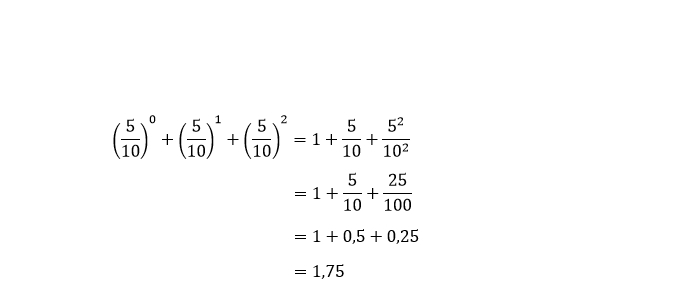
• Pangkat Penjumlahan
  Apabila terdapat perkalian bilangan dengan basis yang sama, maka langkah selanjutnya yakni pangkatnya harus ditambah. Contoh dibawah ini :

a^m x aⁿ = a^{m + n}

Contoh :  2⁴ x 2² = 2^{4 + 2} = 2⁶ = 64

• Pangkat Pengurangan
  Apabila terdapat pembagian bilangan dengan basis yang sama, maka langkah selanjutnya yakni pangkatnya harus dikurang. Contoh dibawah ini :

a^m : aⁿ = a^{m – n}

Contoh : 2⁵ : 2³ = 2^{5 – 3} = 2² = 4

• Pangkat Negatif
  Apabila terdapat bilangan yang menggunakan pangkat negatif, maka nilainya sama dengan 1 per bilangan eksponen tersebut tapi pangkatnya itu sendiri menjadi positif. Contoh dibawah ini :

• Pangkat Nol
  Apabila terdapat bilangan yang berpangkat nol, maka hasilnya sama dengan 1 berapapun nilai bilangan basisnya, akan tetapi dengan syarat bilangan basisnya tidak sama dengan 0. Contoh dibawah ini :

a⁰ = 1, untuk a ≠ 0

Contoh : 

2⁰ = 1

7⁰ = 1

• Bilangan Pecahan
  Adalah suatu bilangan berpangkat yang diakar, maka pangkat dari akarnya dapat ditulis menjadi penyebut dari pangkat bilangannya. Contoh dibawah ini :

• Bilangan Negatif Berpangkat Genap
  Adalah suatu bilangan negatif, yang jika dipangkatkan dengan bilangan genap maka hasilnya adalah bilangan positif. Contoh dibawah ini :

(-a)ⁿ = aⁿ , dengan n = genap

Contoh :

(-2)² = 2²

(-2) x(-2) = 2 x 2

4 = 4

• Bilangan Negatif Berpangkat Ganjil
  Adalah suatu bilangan negatif, yang jika dipangkatkan dengan bilangan ganjil, maka hasilnya adalah bilangan negatif. Contoh dibawah ini :

(-a)^m = -a^m , dengan m = ganjil
Contoh : 
(-2)³ = -(2³)
(-2) x(-2) x(-2) = -(2 x 2 x 2)
-8 = -8

Bilangan Berpangkat Positif

Bilangan berpangkat positif adalah suatu bilangan yang memiliki pangkat dalam bilangan positif atau sering juga disebut eksponen. Dalam bentuk ini x adalah bilangan pokok dan y adalah pangkat. Pangkat itu sendiri adalah jumlah faktor dari bilangan pokok. Contoh soal bilangan berpangkat positif :

Bilangan Berpangkat Negatif

Bilangan berpangkat negatif adalah kebalikan dari bilangan pangkat positif yang merupakan perkalian berulang, dimana pembagian berulang bilangan berpangkat tersebut dengan pengulangan pembagian sejumlah bilangan pangkat negatif yang diinginkan pada soal.

Bilangan Pangkat Nol

Bilangan berpangkat Nol yakni semua bilangan pokok kecuali 0 apabila dipangkatkan dengan 0 maka hasilnya 1.

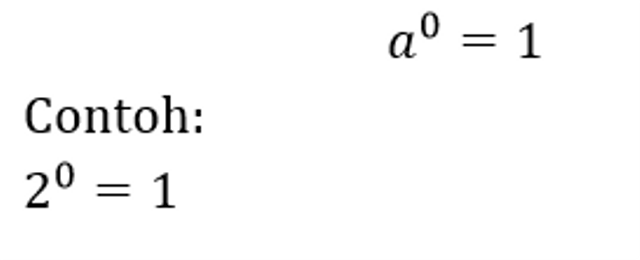
Bilangan Berpangkat Dalam Bentuk Akar

Bilangan berpangkat dalam bentuk akar adalah bilangan yang apabila dimasukkan ke dalam operasi bentuk akar akan menghasilkan bilangan irasional. Bentuk akar tergolong kedalam bilangan irasional yang mana bilangan irasional tidak bisa disebutkan dengan menggunakan bilangan pecahan x/y, x serta y bilangan bulat x dan y tidak sama dengan 0.

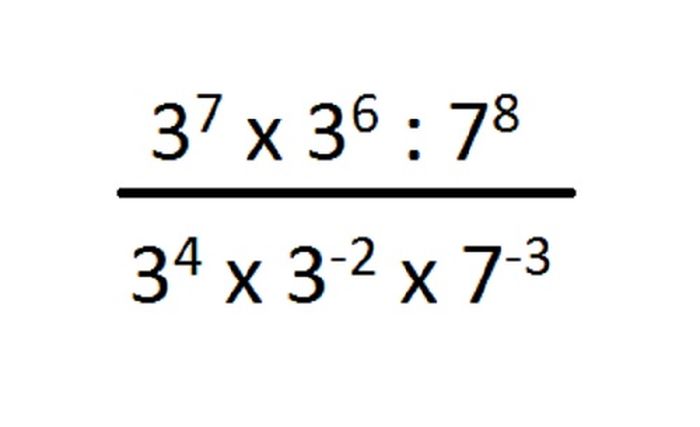
Berikut kami lampirkan file dalam bentuk pdf dan juga bisa untuk diedit :

Kesimpulan

Sebenarnya belajar tentang mata pelajaran matematika tidak begitu sulit tidak seperti apa yang kita bayangkan, asalkan kita rajin dan sering latihan mengerjakan soal-soal. Dengan adanya artikel tentang contoh soal bilangan berpangkat ini, diharapkan pembaca dapat lebih memahami tentang bilangan berpangkat. Dan setelah membaca artikel ini dapat lebih menarik minat pembaca pada suatu bilangan berpangkat.

Untuk anda yang masih bingung dengan bilangan berpangkat, saya menyarankan agar anda mendownload file diatas yang ada di dalam artikel ini.Saya harap artikel ini dapat membantu anda dalam mempelajari bilangan berpangkat, dan lebih menarik minat anda untuk lebih belajar matematika.